Modellierung dynamischer Prozesse mit Differentialgleichungen (DGL) und deren Parameterschätzung mit dem Excel® Solver

Beispiel Bakteriendynamik

Zusammenfassung: Am Beispiel der Bakteriendynamik wird in Excel® mit Hilfe des implementierten Solver die Parameterschätzungen möglicher analytischer Lösungen einer numerisch gelösten Differentialgleichung inkl. Parameterschätzung gegenübergestellt.

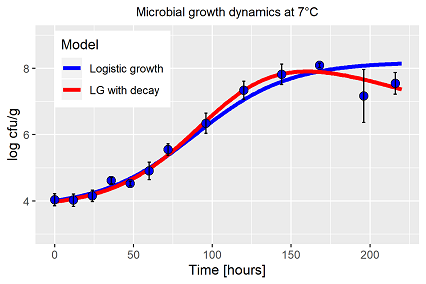
Analytische gelöste Bakteriumwachstumsmodelle — Abb. 1: Modellmöglichkeiten für Bakteriendaten bei konstanter Temperatur, blaue Linie: klassischer Ansatz; rote Linie: Adaption mit Populationsabbau

Interessanterweise wird die logistische Wachstumsfunktion aus dem vorherigen Abschnitt zumeist zur Beschreibung der Wachstumsdynamik von Bakterien herangezogen. Unter idealen Bedingungen auf der perfekten Agarplatte folgt das Zellwachstum, bezogen auf einen kurzen Zeitabschnitt, während seiner verschiedenen Wachstumsphasen (Adaption (Lag-Phase), exponentielles Wachstum, stationäre Phase) diesem Muster. Tatsächlich ist diese Idealdynamik schon bei kleinster Änderung der Temperatur mit Hilfe des logistischen Modells nicht mehr darstellbar. Hinzu kommen, dass nach Erreichen des Maximums die Population wieder abnimmt, z.B. durch selbst-inhibitorische Prozesse, dies ist ebenfalls nicht Bestandteil des logistischen Modells. Der 3. Punkt: Die Bakterienkulturen oder eher die ersten Messwerte starten meist schon mit Werten >10⁴, d.h. die Kurvatur der Lag-Phase ist mit dem Modell ebenfalls nicht so einfach darstellbar und muss durch entsprechende Verzögerungsparameter berücksichtigt werden.

Da über eine Modellanpassung umfangreiche Rückschlüsse auf die Bakterienpopulation gemacht werden, z.B. eine Charakterisierung der Population über den entsprechenden Parametervektor hinsichtlich der experimentellen Versuchsfrage, ist es nur logisch und konsequent, die Gesamtdynamik durch ein entsprechendes Modell abzubilden, und nicht nur den zeitlichen Bereich, der ein bisschen an die logistische Funktion erinnert. In eigenen Arbeiten über das Bakterienwachstum auf Hackfleisch in Abhängigkeit von der Temperatur haben wir selbst den eigenen Anspruch nicht erfüllt (Abb. 1, blaue Linie), die signifikante Abweichungen der letzten beiden Messtermine wurden ignoriert, die Abweichung als unabänderlich dem üblichen Versuchsfehler zugeordnet. Die kommenden Beispiele vorwegnehmend, tatsächlich hat die Population das Maximum bei 7°C schon überschritten, erste Abbauprozesse sind schon eingeleitet (Abb. 1, rote Linie). Dazu ist alternativer Ansatz notwendig, die klassischen Modelle sind nicht in der Lage dazu. Warum ist das von Bedeutung? Tatsächlich ergibt sich aus der Unzulänglichkeit der Verhulst Funktion ein veränderter Wachstumsparameter r, auch haben die beiden letzten Messpunkte den Kapazitätsparameter K beeinflusst, nicht zu vergessen ist dabei auch die hohe Korrelation der Parameter bei diesen Funktionen. Diese Umstände spielen alle eine Rolle, wenn die Population über ihren Parametervektor charakterisiert wird.

Im Folgenden wird entsprechend der Ursprungsdaten¹ mit Zellen pro Einheit gerechnet, wohl wissend, dass CFU/ml oder TVC/ml die allgemein übliche Einheiten mit höherer Aussagekraft wären. Des weiteren wird jetzt nicht explizit wiederholt auf die Berechnungen der logarithmierten Werte hingewiesen, d.h. die folgenden Gleichungen und Graphiken beschreiben den Logarithmus der Populationsgrößen.

Auch für dieses zu modellierende Problem gibt es analytisch gelöste Alternativen, die sowohl das sigmoide Wachstum, als auch den Populationsrückgang während der Stagnationsphase berücksichtigten. Richter et al.² verwenden einen Ansatz mit entsprechender Schaltfunktion, der bei geeigneter Parameterwahl einen exponentiellen Abbau beschreibt.

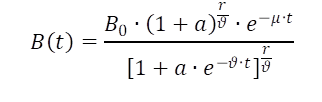
Modell mit Reduktionsterm über Schaltfunktion — Gl. 1: Modell nach Richter et al.² mit Schaltfunktion und Sterbeterm

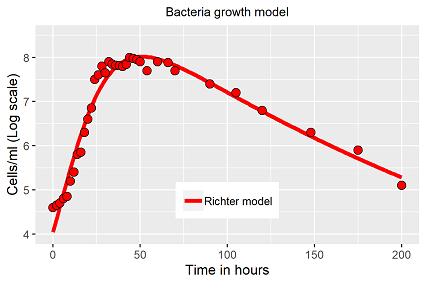
Analytisches Bakteriumswachstumsmodell — Abb. 2: Anpassung von Gl. 1 an die Bakteriendaten, R²=0.96

Das Modell lässt sich an die Bakteriendaten anpassen (Abb. 2), R² ≈ 0.96, exponentielles Wachstum, Verlauf der stationären Phase und der Absterbeverlauf werden sehr gut abgebildet, bei gegebener Ausgangsdichte ist die beobachtete Lag-Phase bei diesem Ansatz nicht modellierbar, bzw. der Anpassungsalgorithmus findet keine Lösung für den vorliegenden Datensatz.

Weniger elegant, aber seinen Zweck erfüllend: man kann den Kapazitätsterm K der klassischen Wachstumsfunktionen (Verhulst, Richards oder modifiziert Logistisch) durch einen exponentiellen Abbauterm ersetzen. Natürlich müssen die Startwerte dieses Terms zum Zeitpunkt t=0 plausibel gewählt werden. Im Falle von Bakteriendichten ist der Kapazitätsterm im Voraus ableitbar, da die physikalische Grenze der Populationsdichte bei ca. 10¹⁰ bis 10¹² pro Volumeneinheit (ml) liegen dürfte. Die Gleichungen an sich sind hier nicht nochmals dargestellt.

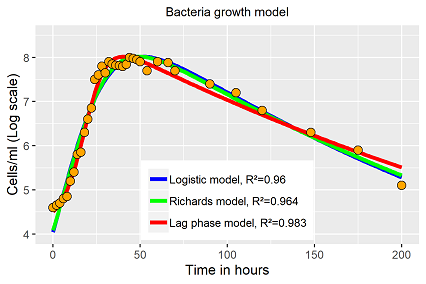
Analytisches Bakteriumswachstumsmodell mit variablem Kapazitätsterm — Abb. 3: Die klassische Wachstumsmodelle mit zeitabhängigem Kapazitätsterm

Alle drei Modelle lassen sich an die Daten mehr oder weniger plausibel anpassen (Abb. 3). Während die Verhulst, als auch die Richardsgleichung, ebenfalls nicht in der Lage sind die Lag Phase adäquat zu berücksichtigen, bildet das Verhulst Derivat mit Lag-Term die Lag- und exponentielle Wachstumsphase nahezu perfekt nach. Dafür wird bei diesem Modell die Stagnationsphase schlechter abgebildet, die Zerfallsphase wird tatsächlich falsch dargestellt, die Residuen dieser Phase weisen auf einen systematischen Fehler hin. Obwohl das Modell den höchsten R²-Wert hat, auch weil der Fit besser ist in den Bereichen höherer Datendichten, bleibt es aber dabei, nur eine kurze Periode der Wachstumsdynamik wird von dem Modell gut abgebildet.

Nachdem es den Anschein hat, dass die bestehenden Modelle teilweise unzureichend sind für die Modellierung der Gesamtdynamik von Bakterienkulturen, verlassen wir den Bereich der analytischen Modelle und entwickeln auf der Basis des Datensatzes folgende Erweiterungen der logistischen Wachstumsfunktion mit zwei Schaltfunktionen. Der Beginn der exponentiellen Phase wird hierbei explizit angeschaltet, wenn eine kritische Zeit erreicht ist, wieder abgeschaltet. Der erste Schalter dient der Berücksichtigung der Lag-Phase, der zweite Schalter leitet in der Konsequenz die Zerfallsphase ein.

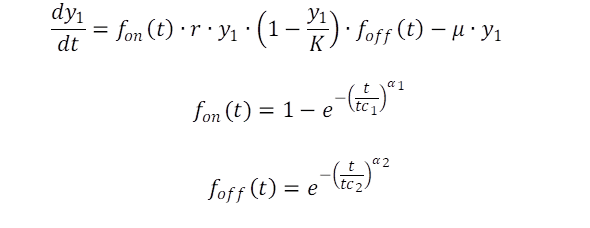
Differentialgleichung der Bakterienwachstumsdynamik — Gl. 2: DGL eines optimierten Bakterienmodells mit Schaltfunktionen

Der Nutzen der Schaltfunktionen ist klar: Es geht um die Berücksichtigung der Adaptionsphase bevor das Wachstum mit der vorgegebenen Rate r einsetzt, d.h. die exponentielle Phase wird eingeleitet wenn sich die Zeit dem kritischen Wert tc₁ nähert. Im umgekehrten Fall, wenn sich die Zeit dem kritischen Wert tc₂ nähert und die Population mit der Rate μ sinkt, bzw. stirbt. Der Retardationsterm (1-y₁/K) ist theoretisch zwar vernachlässigbar, in Bezug auf die vorliegenden Daten wird die Stagnation in dem entsprechenden Zeitfenster berücksichtigt.

Video 1: Parameterschätzung von Gl. 2 bei gegebenen Startwerten mit dem Solver, Ausführung über den Solver VBA Code. Beachten Sie den Anpassungsfortschritt des Solver unten links im Ausgabebalken von Excel. Anhand der Anzahl der Iterationen lässt sich die Komplexität des Anpassungsproblems erkennen.

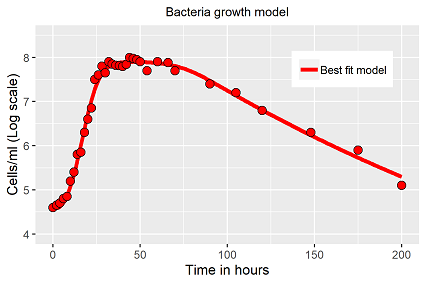
DGL Bakteriumswachstumsmodell mit Schaltfunktionen — Abb. 4: Anpassung der DGL mit 2 Schaltfunktionen, R²=0.994

Für den Fall das Video kann nicht abgespielt werden, Abb. 4 verdeutlich das Anpassungsergebnis an die Differentialgleichung (Gl. 2)

Auch wenn die Anpassung perfekt erscheint (Abb. 4), es muss erwähnt werden, dass die Lösung nicht einzigartig für dieses Modell ist (wie so oft), sogar abhängig ist von der Wahl der Startparameter. Man hat vom Modellprinzip mehrere Optionen: Die Schaltfunktionen beschreiben einen sanften Übergang indem man kleine Exponenten wählt (~2) oder einen scharfen Übergang mit hohen Exponenten (~35), beide führen zu einer Lösung mit ähnlicher Güte (R²>0.99), aber verschiedenen Parametervektoren. In einem direkten Vergleich verschiedener Population ist dieser Umstand zu berücksichtigen.

Literatur:
¹Daten entnommen aus Rathmann (2012),Parameterschätzung in gewöhnlichen Differentialgleichungen, SAXSIM 2012;
²Richter & Söndgerath (1990), Parameter estimation in ecology, VCH Weinheim, 218 pp