Project
Differential equations
&
parameter estimation

• Introduction
• Fitting demo
• Quality check
• Bacteria growth dynamics
• Yellow rust dynamics
• Melon growth dynamics
• Model & RKF download

Modeling dynamical processes with differential equations (ODE's) and parameter fitting
by using the Excel® Solver

Quality check

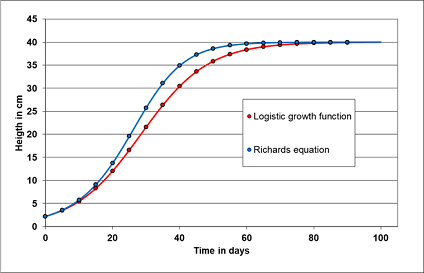
To check the precision of the numerical integration of the ODE's, the outcome of the analytical solution with a given set of parameters (see table 1) of widely used differential equations, as the logistic growth function and the Richards function, are contrasted to the numerical solutions of the RKF method of both differential equations (fig. 1). The maximum deviance is in the range 1E-8.

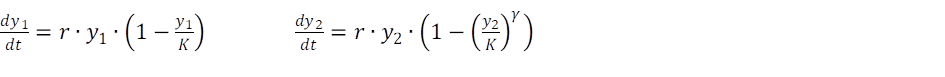
The related VBA code:
dy(1) = r * y(1) * (1 - y(1) / K)
dy(2) = r * y(2) * (1 - (y(2) / K) ^ gamma)

The second check is the accuracy of the estimated parameters for both the analytical and numerical solution of both ODE's.

Table 1: Parameter comparison of fitted ODE-models to first the analytical models and second to numerical solved models

The results show minor deviance from the exact target value, while the fit to the numerical solution appears marginal poorer compared to the fit to the analytical solution of both models. It is up to the user whether such uncertainties of the fitting process are acceptable for his needed precision.

It is possible to get false fitting results, if the initial values of these specific equations are poorly chosen (fig. 2). Even division zero overflows might happen if for example the growth rate is set larger than the capacity term, or one of the parameters approaches to zero. As both equations behave chaotic above certain parameter combinations, those situation should be prevented. Set the side conditions of Solver with respect to model shape might help to avoid such fits to apparent local optima. Lastly, it is recommended to repeat Solver with the first solution. Sometimes it will improve the result, as time and iteration overflow might have occurred in the first fit.