Fallbeispiel 3: Auswertung einer einfaktoriellen Versuchsanlage mit 3 Faktorstufen
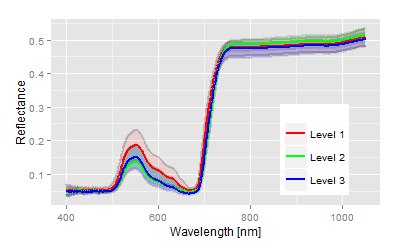
Als Beispiel dienen die Spektren einer einfaktoriellen Anlage (mit Behandlungseffekt als Faktor mit 3 Stufen, bzw. 3 Merkmalen dieses Faktors, Faktor ist diskret)
Fragestellung: Gibt es einen Unterschied zwischen den drei Merkmalen? Wenn ja, welche Merkmale unterscheiden sich in welcher Größenordnung?
Zusammenfassung und Erläuterung der statistischen Parameter
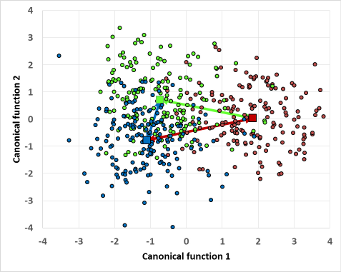
| Statistische Parameter | Erläuterung: Für die Auswertung mehrerer Faktorstufen im Umfang n werden entsprechend der Anzahl der Faktorstufen n-1 Diskriminanzfunktionen benötigt und getestet, ebenfalls wird die kanonische Korrelation entsprechend aufgeteilt. Dargestellt werden die Werte der Diskriminanzfunktionen im 2D/3D Raum, auch wenn sich Koordinaten höherer Ordnungen ergeben können. Das hängt von der Komplexität der Versuchsanlage ab. Die kanonischen Distanzen beschreiben die mittleren Vektoren in der Diskriminanzfläche, bzw. -raum. | |
| Wilks-Lamda | P=0.000 | Diskriminanzfunktionen sind signifikant, d.h. es gibt einen hoch signifikanten Unterschied zwischen den 3 Merkmalen. |
| kanonische Korrelation | 0.79 und 0.53 | Die Korrelation ist hoch für die erste Diskriminanzfunktion auf der Skala von 0 bis 1, auch hier, der Unterschied ist deutlich. Für die 2. Diskriminanzfunktion ist die Korrelation geringer, aber der Anteil der erklärten Varianz für die zweite Funktion liegt gerade mal bei 20%. |
| kanonische Distanzen | 2.74 | Die kanonischen Distanzen lassen n Vergleiche zu: Level 1 nach Level 2 ist im Bereich von 2.7 (***), von Level 1 nach Level 3 im Bereich von 3.1 (***) und von Level 2 nach Level 3 bei 1.5 (n.s.) auf der Skala der kanonischen Distanzfläche. Level 1 unterscheidet sich wesentlich von 2 und 3, der Unterschied zwischen den Merkmalen 2 und 3 ist mit 1.5 wesentlich schwächer ausgeprägt und nicht signifikant. |
| Klassifikation | 82% | Hoch, man kann die drei Merkmale gut klassifizieren. |
ANOVA Tabelle für obige Spektren
| Parameter | A | B1 | AC1 | BC1 | AL1 | BE1 | B2 | AC2 | BC2 | AL2 | BE2 | B3 | AC3 | AL3 |
| F-Wert | 26.9 | 17.5 | 54.5 | 46.1 | 8.6 | 5.1 | 0.6 | 60.3 | 42.8 | 3.9 | 55.4 | 29.4 | 24.4 | 62.6 |
| p-Wert | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.006 | 0.554 | 0.000 | 0.000 | 0.021 | 0.000 | 0.000 | 0.000 | 0.000 |
Zusammenfassung
Die 3 Merkmale lassen sich anhand der Spektren sehr gut unterscheiden, die statistischen Parameter ergeben ein eindeutiges Bild. Die F-Werte der ANOVA für die Parameter zeigen, dass sich die Spektren in nahezu allen Wellenlängenbereichen signifikant unterscheiden. Es bedeutet aber nur, dass es einen Unterschied gibt. Welche mittleren Spektren sich genau unterscheiden, lässt sich über die Distanzen in der kanonischen Fläche demonstrieren. Die Distanzen der Merkmalszentren zueinander ergeben ein relatives Maß, welches die Unterschiede der Faktorstufen (= Merkmale) auf dieser dimensionslosen Skalenebene quantifiziert. Unter Einbehaltung eines erweiterten Sicherheitsniveaus muss man davon ausgehen, dass sich Faktorstufe 2 und 3 nicht unterscheiden. Auch wenn es hier sicherlich Grenzen in der Aussagekraft gibt, man hat ein Äquivalent zu den multiplen Mittelwertvergleichstests der klassischen ANOVA.
 Evaluation reinvented
Evaluation reinvented
